该计算假定BEP处的固定旁通流量为流量的10%,设计时控制阀的压降固定为行程的70%。控制阀具有理想的等百分比特性,量程分别为25和50。
计算结果如图4所示,该结果基于泵的特性曲线I。相对最大流量相对于A(设计时控制阀的相对压降)作图。参数B构成系统的相对动态压力损失。如曲线II所示,基于泵的特性进行了相同的计算(见图5)。
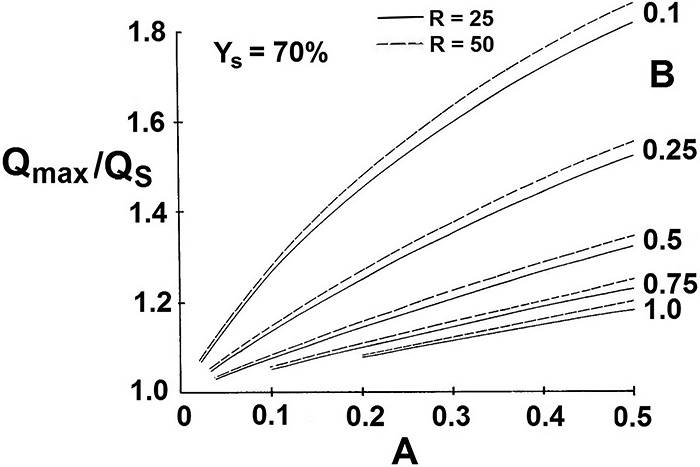
图4.最大流量取决于控制阀的相对压力损失,变量A基于图2的曲线I。参数B表示系统的相对动态压力损失。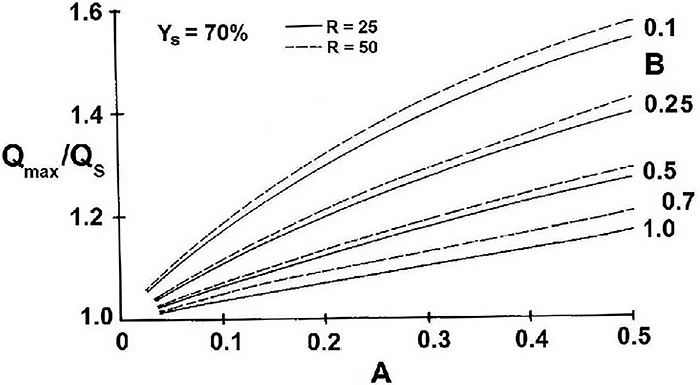
图5.最大流量取决于控制阀的相对压力损失,变量A基于图2的曲线II。参数B表示系统的相对动态压力损失。
通过对这些数字进行比较,可以看出泵的特性对最大流量的巨大影响:在给定的控制阀相对压降下,越平坦,最大流量就越大。将控制阀的可调范围加倍会使最大流量增加一小部分。
可以通过具有类似于图1中的系统的配置的另一个示例来突出显示先前的场景,在该示例中,低量程比的控制阀(基本情况)被具有较高量程的控制阀替代。
图6中的HQ图包含泵的特性和系统的压降曲线,而不会损失控制阀。
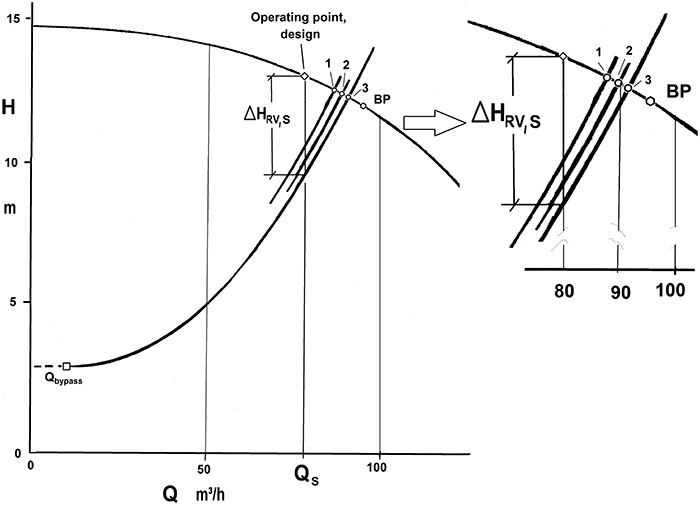
图6.控制阀的可调节性对最大流量的影响示例。
添加控制阀的压力损失,已被固定到ΔH RV在Y处的一个无量纲的行程=3米小号 = 70%,结果在工作点1(基础情况)相匹配的设计流速和10μm的旁路3 /小时。
图6中的曲线图显示了几种情况,由于不同的控制阀的可调范围,工作点处于各种最大流量下。最大流量Q S由行程100%(完全打开的控制阀)确定。
使用适当的额定Cv计算具有不同调节阀可变性的系统的压力损失曲线,将其转换为摩擦损失因数,随后将其用于伯努利方程式。
摩擦损耗因数随量程的增加而减小;在极端情况下,它或多或少地等同于具有阀门长度的全孔管。
基于设计流量Q S,关系Q max / Q S可以从图6中得出:
· 点1(基本情况):R = 25;Q 最大 / Q 小号 ≈109%与控制阀的线性特性
· 点2:R = 25;Q 最大 / Q 小号 ≈为等百分比特性113%
· 点3:R = 150;Q 最大 / Q 小号 ≈为等百分比特性-的直管114%置换导致Q中的控制阀最大 / Q 小号 ≈115%的
此示例说明,高量程比通常不会产生很大影响,但是此结果取决于单个系统和所选参数。
此外,在控制阀的设计压力损失和设计行程相同的情况下,由于Cv急剧增加,因此等百分比阀的特性允许更高的最大流量。
但是,每当行程接近100%时,由于行程的微小变化会引起流量的较大变化,因此可控性可能会下降。
结论
定性地,泵的特性下降越陡,最大流量越小,系统的相对动压损失越高,最大流量越小。
控制阀的参数“设计流量”和“设计压力损失及行程”确定了参考值。因此,例如将指定的设计流量增加10%,而又不增加泵输送的压力,这并不意味着系统必然会达到该流量。
参考文献
1. Yu,FC,“估算实际控制阀压降的简便方法”,第45-48页,烃加工,2000年8月
2. G. Unnikrishnan,“轻松可视化泵和控制阀的相互作用”,第51-56页,烃加工,2007年8月
3. WA Jerdal等人,“特定转速nq = 20…80的泵的无量纲特性”,第546-550页,交易ASME,第1卷。124,2002年6月
4. Green,DW,Perry RH,“ Perry的化学工程师手册”,第8版,第8节,p。8-83



